Скрытые измерения реальности: от сферы до космоса

Представьте на мгновение, что вы — двумерное существо, живущее на поверхности сферы. Вы можете двигаться в любом направлении, измерять расстояния, строить фигуры. Но у вас нет никакого представления о третьем измерении. С вашей точки зрения, мир кажется бесконечным, потому что вы можете идти вечно, не достигая края. Однако если вы начнете строить большие треугольники и измерять их углы, вы обнаружите нечто странное: сумма углов всегда оказывается больше 180 градусов. Постепенно вы поймете, что ваш мир искривлен. Так начинается путешествие в геометрию искривленных пространств — миров, где интуиция подводит, а математика открывает истины, скрытые от непосредственного восприятия.

Сферы: геометрия нашей планеты

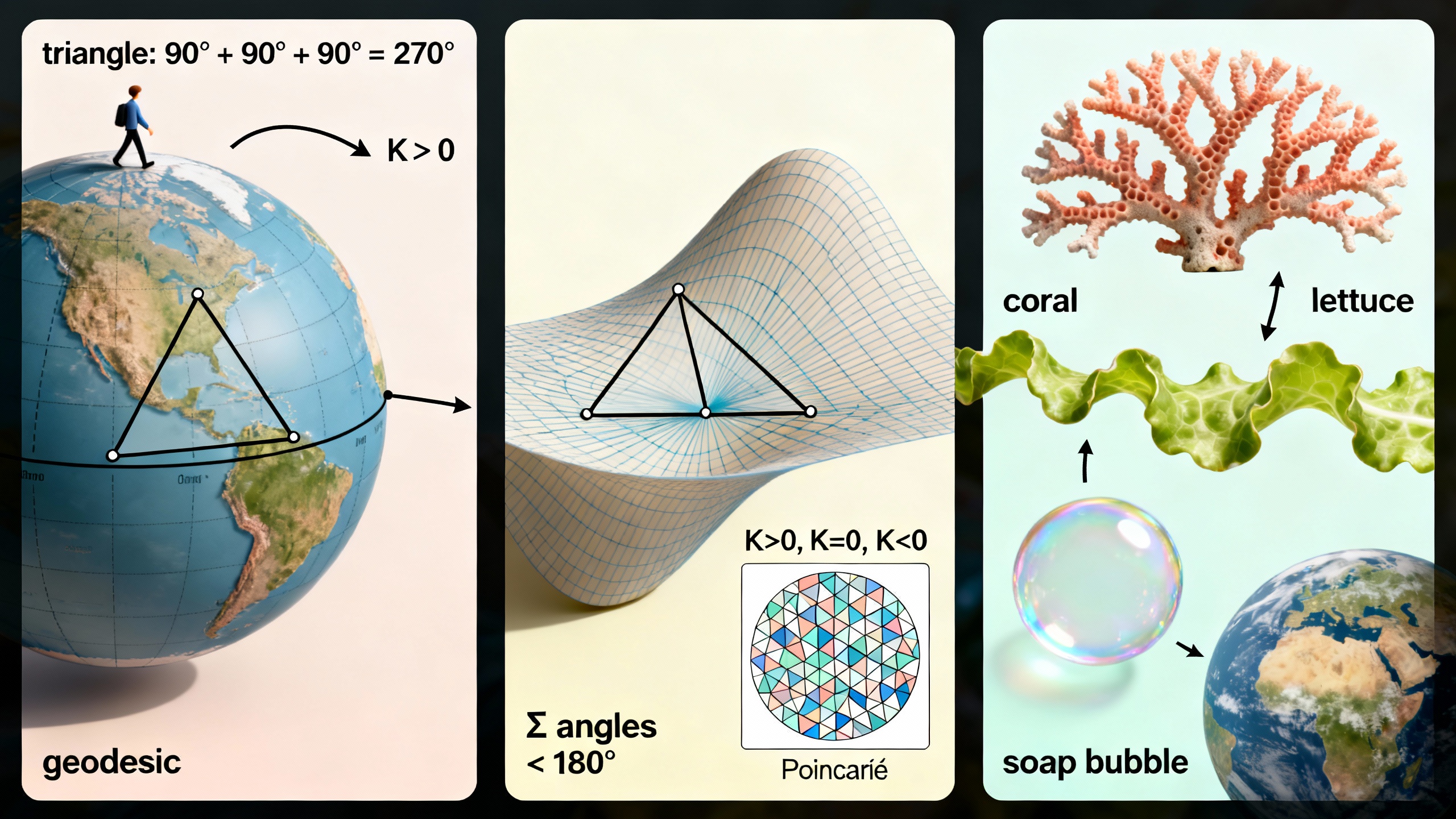
Геометрия сферы знакома каждому, кто изучал географию Земли. Хотя мы часто рисуем карты на плоских листах бумаги, истинная поверхность нашей планеты искривлена. Кратчайший путь между двумя точками на Земле — это не прямая линия на карте, а сегмент большого круга, такого как экватор или меридиан. Эти пути, называемые геодезическими, действуют как «прямые линии» сферической геометрии, но их поведение радикально отличается от прямых на плоскости.

На плоской поверхности две геодезические могут быть параллельными вечно, как железнодорожные пути, которые никогда не встречаются. На сфере же каждая пара больших кругов в конечном итоге пересекается. Линии долготы начинаются далеко друг от друга на экваторе, но встречаются на обоих полюсах. В сферической геометрии истинных параллелей вообще не существует.

Треугольники на сфере также отказываются следовать евклидовым правилам. Если вы нарисуете треугольник с тремя углами по 90 градусов — используя экватор и две линии долготы — вы получите фигуру, углы которой в сумме дают 270 градусов. Это невозможно в плоской геометрии, где сумма всегда должна равняться 180 градусам. На сфере сумма углов треугольника всегда больше 180 градусов, и это превышение увеличивается с площадью треугольника.

Это наблюдение создает мост между геометрией и измерением. Если бы вы были древним мореплавателем, у вас могло бы не быть языка неевклидовой геометрии, но вы бы все равно заметили, что долгие плавания следуют дугам, а не прямым линиям. Моряки знали, что кратчайший маршрут через Атлантику — это не прямой курс на прямоугольной карте, а изогнутый путь вдоль большого круга. Современные пилоты полагаются на тот же принцип при прокладке межконтинентальных маршрутов.

Седла и гиперболы: миры отрицательной кривизны

Если сферическая геометрия относительно легко визуализируется, то гиперболическая геометрия представляет гораздо больше трудностей, потому что ее естественные поверхности не могут быть полностью представлены в плоском пространстве. Тем не менее, седло дает нам представление о том, как она выглядит.

Лошадиное седло изгибается вверх в одном направлении и вниз в другом. В отличие от сферы, которая изгибается одинаково во всех направлениях, седло обладает отрицательной кривизной. В такой геометрии геодезические расходятся быстрее, чем в евклидовом пространстве. Через данную точку можно провести бесконечно много линий, которые никогда не пересекутся с данной прямой. Это делает гиперболическое пространство полной противоположностью сферическому.

Треугольники в гиперболической геометрии также ведут себя странно. Сумма их углов всегда меньше 180 градусов, и чем больше треугольник, тем меньше становится эта сумма. Если представить треугольник настолько большой, что его стороны почти простираются до бесконечности, его углы могут сжиматься почти до нуля.

Формы искажаются в гиперболическом пространстве так быстро, что целую бесконечную плоскость можно представить в конечном круге, причем фигуры уменьшаются все больше и больше по мере приближения к границе. Этот тип представления, известный как модель диска Пуанкаре, — один из самых мощных способов, которыми математики и художники пытались осмыслить гиперболические миры.

Кривизна: ключ к классификации пространств

Различие между сферической, гиперболической и евклидовой геометриями заключается не в правилах логики, а в кривизне пространства. Кривизна может быть:

• Положительной — как на сфере
• Отрицательной — как на седле
• Нулевой — как на плоскости

Каждый тип кривизны изменяет поведение геодезических, треугольников и параллелизма. Евклидова геометрия — это просто частный случай, когда кривизна равна нулю. Как только эта структура стала ясной, появилась возможность классифицировать целые семейства геометрий на основе знака и величины кривизны.

Это ознаменовало глубокий сдвиг в математике. Геометрия больше не была набором жестких истин одной системы, а превратилась в исследование полного спектра возможных пространств.

Природа как геометр

Искривленная геометрия — это не просто математическая абстракция. Природа постоянно использует эти принципы, часто удивительным образом.

Коралловые рифы строят структуры, которые расходятся наружу с волнистыми поверхностями, напоминающими гиперболические мозаики. Эти формы максимизируют площадь поверхности для питания, оставаясь компактными по объему. Биологи обнаружили, что математика гиперболических поверхностей замечательно точно описывает рост коралловых колоний.

Листья салата и капусты демонстрируют гиперболическую геометрию в своих волнистых краях. Эти формы возникают потому, что края листьев растут быстрее, чем их центры. Когда поверхность растет больше на границе, чем внутри, она не может оставаться плоской — она принимает форму с отрицательной кривизной.

Мыльные пузыри образуют почти идеальные сферы, потому что поверхностное натяжение минимизирует площадь поверхности для данного объема, а сфера — наиболее эффективное решение. Планеты и звезды под действием гравитации также становятся сферическими, когда они достаточно массивны, чтобы их материал мог осесть в равновесие.

Что особенно поразительно, математики когда-то считали невозможным то, что природа регулярно использует как решение. Формы, которые выглядят как искусство, на самом деле являются естественными следствиями дифференциального роста и физических ограничений.

Риман и революция в понимании пространства

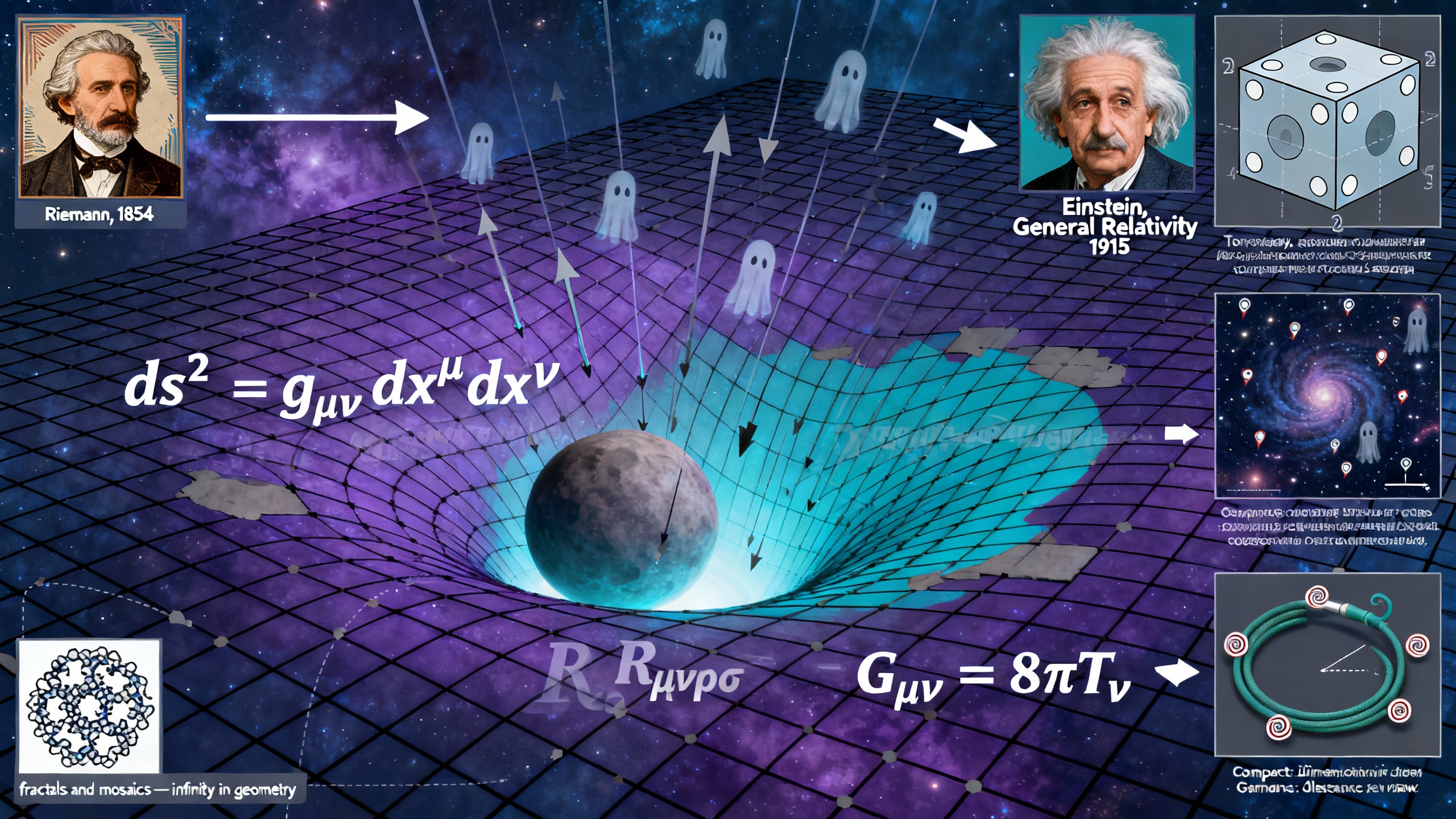
Настоящий прорыв в понимании искривленных пространств произошел благодаря Бернхарду Риману. В своей знаменитой лекции 1854 года он предложил радикально новый взгляд на геометрию. Вместо того чтобы предполагать, что пространство плоское и евклидово, Риман предложил, что геометрия должна основываться на идее многообразия — пространства, которое в малых масштабах выглядит как евклидово пространство, но в больших масштабах может иметь кривизну.

Например, поверхность Земли выглядит плоской, когда вы стоите в поле, но при удалении обнаруживается, что она сферическая. Риман распространил эту идею на более высокие измерения: пространство может быть локально плоским, но глобально искривленным, и правила геометрии могут меняться в зависимости от этой кривизны.

Что сделало подход Римана революционным, это то, что он предоставил способ математического описания кривизны. Он показал, что можно определить метрику — функцию, определяющую расстояния между точками, — и что свойства этой метрики кодируют форму пространства.

Риман также подчеркнул, что геометрия — это не только вопрос логики или абстрактной конструкции, но и физической реальности. Он утверждал, что истинная геометрия пространства — это эмпирический вопрос, который должен решаться наблюдением и измерением. Это был радикальный отход от веков философии.

Эйнштейн: гравитация как геометрия

Полное значение идей Римана не было осознано до тех пор, пока физика не догнала математику. Связь возникла благодаря Альберту Эйнштейну более чем через полвека. Когда Эйнштейн разрабатывал свою теорию общей теории относительности в 1915 году, ему нужна была математическая структура, способная описать гравитацию не как силу, а как кривизну пространства-времени.

Именно геометрия Римана предоставила решение. Метрика стала способом описания структуры пространства-времени, а тензор кривизны Римана стал языком для выражения того, как масса и энергия искривляют это пространство-время. Сам Эйнштейн признавал, что без работы Римана его теория была бы невозможна.

Революция Римана была не только математической, но и концептуальной. Она переопределила, что значит для пространства иметь форму. Вместо того чтобы думать о геометрии как о чем-то, навязанном человеческой интуицией или набором аксиом, он показал, что геометрия — это свойство Вселенной, которое можно изучать эмпирически.

Космология и форма Вселенной

Сегодня космологи активно изучают вопрос: какова истинная геометрия нашей Вселенной? Наблюдения показывают, что Вселенная почти плоская, но это не определяет ее топологию. Космос может быть бесконечным, простираясь бесконечно во всех направлениях, или он может быть конечным, но неограниченным — как поверхность сферы.

Одна из возможностей состоит в том, что Вселенная имеет топологию трехмерного тора. Представьте пространство, обернутое как куб с противоположными гранями, отождествленными так, что выход через одну грань возвращает вас через противоположную. В такой Вселенной свет мог бы обойти космос несколько раз, создавая «призрачные» изображения галактик.

Астрономы искали повторяющиеся узоры в космическом микроволновом фоне — послесвечении Большого взрыва — которые могли бы указывать на такую топологию. Пока убедительных доказательств не найдено, но сам поиск показывает, как радикально глобальная концепция может быть проверена кропотливыми наблюдениями локального света.

От кораллов до галактик: единство принципов

То, что начиналось как абстрактный отход от Евклида, стало объединяющим принципом во всех дисциплинах. Математика кривизны и неевклидовой геометрии объясняет:

• Почему коралловые рифы образуют волнистые структуры
• Почему мыльные пузыри округляются
• Почему галактики группируются в определенные узоры
• Почему свет искривляется вблизи массивных объектов

Она показывает нам, что геометрия не ограничена классной доской, но встроена в живую, растущую и расширяющуюся Вселенную. Каждый пример напоминает нам, что человеческая интуиция — это только одна линза, и что реальность гораздо более гибкая и изобретательная, чем наш разум первоначально представлял.

Бесконечность в геометрии: мозаики и фракталы

Геометрия также распространяется на область бесконечности, где узоры повторяются бесконечно, а поверхности простираются за пределы нашего воображения. В изучении мозаик и фракталов математика дает представление о структурах, которые одновременно бесконечно сложны и удивительно просты.

В евклидовой геометрии мозаики знакомы: квадраты, треугольники и шестиугольники аккуратно покрывают плоскость. Но в гиперболической геометрии мозаики ведут себя иначе. Гиперболическую плоскость можно заполнить правильными многоугольниками в комбинациях, которые были бы невозможны в плоском пространстве. Например, можно замостить гиперболическую плоскость семью правильными шестиугольниками, встречающимися в каждой вершине — что невозможно в евклидовой геометрии.

Фракталы предлагают другой путь в бесконечность. Фрактал — это структура, которая повторяет свою форму во все меньших и меньших масштабах, демонстрируя самоподобие. Самый известный пример — множество Мандельброта. При приближении к его границе открывается бесконечный каскад деталей — формы, похожие на исходную, появляются снова и снова, каждая окружена своими сложными украшениями.

Фракталы изобилуют в природе: ветвление деревьев, структура легких, прожилки листьев, узоры рек и даже распределение галактик демонстрируют фрактальные свойства. Эти структуры часто возникают из простых правил, повторяющихся много раз — рекурсия естественным образом ведет к фрактальным и неевклидовым структурам.

Высшие измерения: за пределами видимого

Математика геометрии применима в любом числе измерений. Одним из самых известных высокоразмерных объектов является тессеракт, или четырехмерный аналог куба. Мы не можем полностью визуализировать его, но можем проецировать в трехмерное пространство, получая искаженные изображения с меньшими кубами, вложенными в большие.

Физика также приняла высшие измерения. Теория струн предполагает, что фундаментальные частицы — это крошечные вибрирующие струны, и что их вибрации требуют существования дополнительных измерений. В зависимости от версии теории, Вселенная может иметь 10 или 11 измерений, большинство из которых «компактифицированы» — свернуты настолько мелко, что не могут наблюдаться напрямую.

Идея компактифицированных измерений тонка. Представьте длинный садовый шланг, рассматриваемый издалека — он выглядит как одномерная линия. Но вблизи видно, что шланг имеет круглое поперечное сечение, добавляющее скрытое измерение. Точно так же физики предполагают, что дополнительные измерения могут существовать в каждой точке пространства, но свернуты так плотно, что мы не можем обнаружить их современными технологиями.

Что геометрия говорит о реальности

Путешествие от прямых линий до искривленных пространств, от двух измерений до десяти, от сфер до фракталов показывает нам фундаментальную истину: пространство не является пассивной сценой, на которой разворачиваются события — оно активный участник космической драмы.

Геометрия перестала быть набором абсолютных истин и стала гипотезой о мире, проверяемой наблюдениями. Какую геометрию выбирает космос — вопрос не логики, а измерения. И то, что мы обнаружили, превосходит самые смелые фантазии наших предков:

• Пространство-время искривляется вблизи массивных объектов
• Вселенная может быть конечной, но неограниченной
• Могут существовать скрытые измерения, свернутые за пределами восприятия
• Природа использует гиперболическую геометрию в своих творениях
• Бесконечность может быть сжата в конечную форму

Все это учит нас смирению. Наши чувства эволюционировали для навигации в ландшафтах, где евклидовы приближения работают достаточно хорошо. Но Вселенная не связана нашими интуициями. Математика расширяет наш охват, давая нам способ постичь непостижимое.

И в этом осознании есть своя красота. Как писал физик Джон Арчибальд Уилер: «Пространство-время говорит материи, как двигаться; материя говорит пространству-времени, как искривляться». Это танец, в котором геометрия и физика неразрывно переплетены, создавая космос одновременно упорядоченный и удивительный, предсказуемый и полный тайн.