Когда прямые линии отказываются подчиняться: революция в понимании пространства

Более двух тысячелетий человечество было уверено, что геометрия — это нечто незыблемое и абсолютное. Треугольники всегда имеют сумму углов в 180 градусов, параллельные прямые никогда не пересекаются, а кратчайший путь между двумя точками — это прямая линия. Эти истины казались настолько очевидными, что философы считали их частью самой структуры человеческого разума. Однако история науки полна моментов, когда то, что казалось незыблемым, рассыпается под натиском новых открытий. Одним из таких моментов стало осознание того, что евклидова геометрия — лишь один из возможных способов описания пространства.

Загадка пятого постулата

Когда древнегреческий математик Евклид около 300 года до нашей эры составлял свои знаменитые «Начала», он заложил основу того, что мы сегодня называем евклидовой геометрией. Его труд строился на пяти постулатах — утверждениях, которые принимались без доказательств. Первые четыре казались предельно ясными: можно провести прямую между любыми двумя точками, можно продлить эту прямую до бесконечности, можно начертить круг с любым центром и радиусом, и все прямые углы равны между собой.

Но пятый постулат выделялся своей сложностью. По сути, он утверждал, что через точку, не лежащую на прямой, можно провести ровно одну прямую, параллельную данной. Это свойство казалось менее самоочевидным, чем остальные, и на протяжении веков математики подозревали, что его можно вывести из первых четырых постулатов. Если бы это удалось, вся геометрия стала бы более элегантной, опираясь на меньшее количество аксиом.

Попытки доказать параллельный постулат продолжались почти два тысячелетия. Блестящие умы от античности до Нового времени бились над этой задачей, создавая изощренные логические конструкции. Средневековые исламские математики, такие как Насир ад-Дин ат-Туси и Омар Хайям, исследовали свойства четырехугольников с равными сторонами и углами, надеясь через них прийти к доказательству. В XVIII веке итальянский математик Джироламо Саккери посвятил целый трактат попыткам доказать пятый постулат методом от противного.

Рождение невозможного: неевклидовы геометрии

Переломный момент наступил в XIX веке. Карл Фридрих Гаусс, один из величайших математиков всех времен, в своих личных записях признавал, что пятый постулат, возможно, невыводим из остальных. Однако он не решился опубликовать свои находки, опасаясь скандала в мире, все еще убежденном в абсолютности евклидовой геометрии.

Более смелыми оказались Николай Лобачевский и Янош Бойяи. Работая независимо друг от друга, они показали нечто революционное: если заменить пятый постулат Евклида на альтернативный, можно построить полностью последовательную систему геометрии. В геометрии Лобачевского через точку, не лежащую на прямой, можно провести бесконечно много прямых, которые никогда не пересекутся с исходной. Это стало основой гиперболической геометрии.

Чтобы понять, насколько это было шокирующим открытием, представьте, что вся ваша жизнь вы считали, что параллельные прямые никогда не встречаются — и вдруг оказывается, что это лишь одна из возможностей. На поверхности сферы, например, «прямые» линии (геодезические) — это дуги больших кругов, как экватор или меридианы. Два меридиана на экваторе кажутся параллельными, но по мере продвижения к полюсам они неизбежно сходятся и пересекаются. Это сферическая геометрия, где параллельных прямых не существует вообще.

Три мира, три геометрии

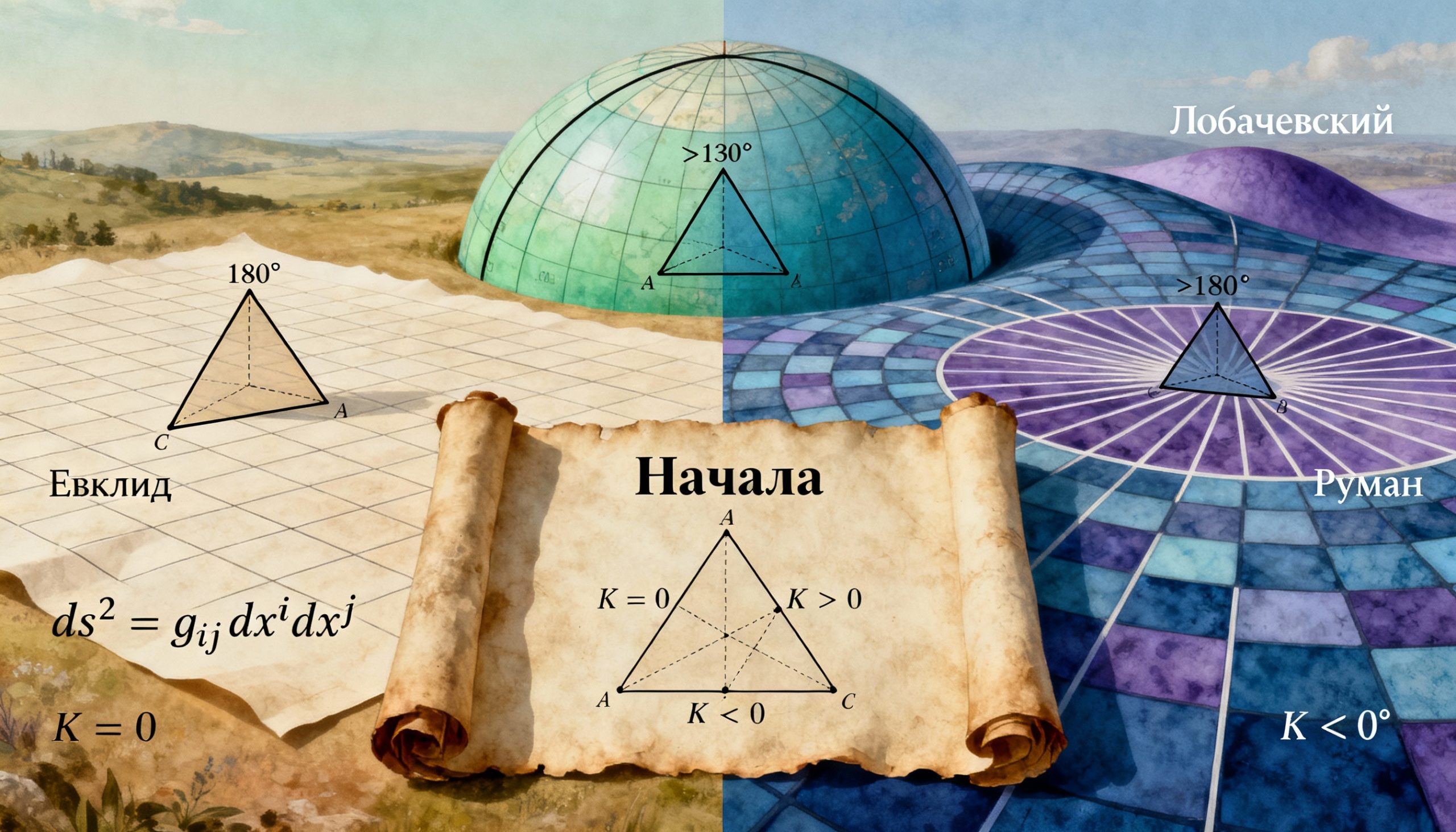
Так возникло понимание трех фундаментально различных типов геометрии, каждая из которых определяется кривизной пространства:

• Евклидова геометрия — плоское пространство с нулевой кривизной, где сумма углов треугольника равна 180°, и существует ровно одна параллельная прямая
• Сферическая геометрия — пространство с положительной кривизной, где сумма углов треугольника больше 180°, и параллельных прямых не существует
• Гиперболическая геометрия — пространство с отрицательной кривизной, где сумма углов треугольника меньше 180°, и существует бесконечно много параллельных прямых

Евклидова геометрия оказалась не универсальной истиной, а лишь частным случаем — случаем, когда кривизна равна нулю. Это открытие перевернуло представления о природе математики и пространства.

От абстракции к реальности

Поначалу неевклидовы геометрии казались чисто математическими курьезами, интересными упражнениями для ума, но далекими от реальности. Однако вскоре стало очевидно, что они описывают наш мир гораздо точнее, чем предполагалось.

Мореплаватели и пилоты давно знали, что кратчайший путь между двумя точками на Земле — это не прямая на плоской карте, а дуга большого круга. Перелеты через Атлантику следуют этим изогнутым траекториям не из-за прихоти, а потому что Земля — сфера, и на ее поверхности действует сферическая геометрия. То, что казалось искривленным путем на плоской карте, на самом деле является самым прямым маршрутом на искривленной поверхности.

Гиперболическая геометрия, хотя и труднее для визуализации, также нашла свои проявления. Форма седла — классический пример поверхности с отрицательной кривизной. Такие формы встречаются в природе чаще, чем можно подумать: от коралловых рифов до листьев салата, от грибных шляпок до складок человеческого мозга.

Прорыв Римана: пространство само может искривляться

Настоящая революция произошла в 1854 году, когда немецкий математик Бернхард Риман прочитал лекцию «О гипотезах, лежащих в основании геометрии». Риман предложил радикально новый взгляд: геометрия — это не набор неизменных истин, а свойство самого пространства, которое можно измерить и изучить экспериментально.

Он ввел понятие многообразия — пространства, которое в малых масштабах выглядит евклидовым, но в больших может обладать кривизной. Представьте, что вы стоите в поле — земля кажется плоской. Но если отдалиться достаточно далеко, становится очевидно, что Земля — сфера. Риман показал, что эта идея применима к пространствам любого числа измерений, и предложил математический аппарат для описания кривизны.

Что особенно важно, Риман утверждал, что истинная геометрия пространства — это эмпирический вопрос, который должен решаться наблюдениями, а не априорными рассуждениями. Это был прямой вызов философии Канта, считавшего евклидову геометрию встроенной в саму структуру человеческого восприятия.

Эйнштейн и геометрия Вселенной

Более полувека идеи Римана оставались преимущественно в области чистой математики. Но в 1915 году Альберт Эйнштейн нашел им применение, которое навсегда изменило физику. Его общая теория относительности описывала гравитацию не как силу, притягивающую объекты друг к другу, а как искривление самого пространства-времени.

Согласно Эйнштейну, массивные объекты, такие как Солнце, искривляют пространство-время вокруг себя. Планеты не «притягиваются» к Солнцу невидимой силой — они следуют кратчайшим путям (геодезическим) в искривленном пространстве-времени. Яблоко падает не потому, что Земля тянет его, а потому что пространство-время вокруг Земли искривлено внутрь, направляя движение яблока.

Эта теория объяснила давнюю астрономическую загадку — аномалию в орбите Меркурия, которую не могла объяснить ньютоновская механика. Она предсказала, что свет должен искривляться при прохождении вблизи массивных объектов — предсказание, подтвержденное в 1919 году во время солнечного затмения.

Параллельные прямые в повседневной жизни

Сегодня неевклидова геометрия — это не просто теоретическая абстракция. Она влияет на вашу повседневную жизнь способами, о которых вы можете даже не подозревать. Система GPS, которая указывает вам дорогу, должна учитывать как специальную, так и общую теорию относительности. Часы на спутниках идут с другой скоростью, чем часы на Земле, из-за различий в гравитации и скорости движения. Без поправок, основанных на неевклидовой геометрии пространства-времени, GPS-навигация накапливала бы ошибки в несколько километров за день.

Наблюдения гравитационных волн — буквальных колебаний в ткани пространства-времени — подтверждают, что геометрия космоса динамична и изменчива. Первое изображение тени черной дыры, полученное в 2019 году, стало триумфом общей теории относительности и подтверждением того, что пространство действительно искривляется способами, описанными Эйнштейном.

Что это значит для нашего понимания реальности?

Открытие неевклидовых геометрий преподнесло человечеству урок смирения. То, что кажется очевидным и самоочевидным, может оказаться лишь частным случаем, применимым в ограниченных условиях. Наш повседневный опыт происходит в масштабах и при скоростях, где евклидова геометрия работает достаточно хорошо. Но когда мы выходим за эти рамки — к космическим расстояниям, экстремальным гравитационным полям или высоким скоростям — евклидовы правила перестают действовать.

Это открытие также изменило саму природу математики. Математика оказалась не просто отражением самоочевидных истин, а системой логических возможностей. Геометрия не открывается в том же смысле, в котором мы открываем физические факты — она конструируется из аксиом. Некоторые из этих конструкций хорошо соотносятся с реальностью, другие остаются абстрактными, но ни одна не является привилегированной по своей природе.

Красота в искривлении

Неевклидова геометрия вдохновила не только ученых, но и художников. Знаменитый голландский график Мауриц Эшер использовал гиперболические мозаики в своих работах, заполняя круг бесконечно повторяющимися узорами ангелов и дьяволов, которые уменьшаются при приближении к краю. Эти работы не просто визуально поразительны — они математически точны, показывая, что бесконечность может быть сжата в конечную рамку.

В природе гиперболические формы появляются в неожиданных местах: в коралловых рифах, чьи волнистые поверхности максимизируют площадь для питания; в листьях салата, края которых растут быстрее центра, вынуждая поверхность сморщиваться в отрицательную кривизну; в грибах с их радиально расходящимися пластинками.

Путь к пониманию

История параллельных прямых, отказавшихся вести себя так, как от них ожидалось, — это не только история математической фрустрации, но и история освобождения. Осмелившись представить, что пятый постулат может не выполняться, математики узнали, что мир форм и пространств намного богаче, чем они когда-либо предполагали.

Они обнаружили, что само пространство может мыслиться множеством способов, и что наша привычная геометрия — лишь один вариант среди многих. Это осознание подготовило почву для современной физики — изучения Вселенной как искривленного и динамического многообразия.

Возможно, самый глубокий урок этой истории заключается в том, что нечто столь простое, как пара параллельных прямых, может нести в себе такую глубину. Концепция, которая кажется тривиальной в школьных упражнениях, оказалась ключом к открытию совершенно новых геометрий. В этом и заключается тихое чудо математики: самые знакомые идеи иногда скрывают самые глубокие тайны.

Точно так же, как параллельные прямые могут расходиться в неожиданных направлениях, наше понимание реальности продолжает расширяться. Мы живем в эпоху, когда геометрия космоса изучается не только теоретически, но и экспериментально — через наблюдения за изгибанием света вокруг галактик, через детектирование гравитационных волн, через точные измерения космического микроволнового фона.

И в этом постоянном исследовании мы видим, что Вселенная не обязана подчиняться нашим интуитивным представлениям. Но даже когда она отказывается следовать прямым линиям, в ней все еще есть свой скрытый порядок — порядок, который мы можем понять, если будем достаточно смелы, чтобы выйти за пределы очевидного.